🔥 메타코드에서 머신러닝 입문 부트캠프 강의를 듣고 있다. 머신러닝 강의에서 그냥 무지성으로 돌렸던 코드에 대해 깊이 이해하고, 내 손으로 최적의 파라미터를 뽑아내고, 하이퍼파라미터 튜닝도 해보고 싶다. 이번에는 지난 글에서 배웠던, 분산과 편향 사이의 trade-off를 해결할 수 있는 방법을 몇 가지 배운다. 현업에서도 활용할 부분이 있으니 잘 정리해 두어야지!
4. 편향(Bias)과 분산(Variance) - 어떻게 Trade-off 문제를 해결할 수 있을까?

지난 글에서, 분산은 과적합(over-fitting)과, 편향은 과소적합(under-fitting)과 관련이 있다고 배웠다.
일반적으로는 분산과 편향이 trade-off 관계라 배웠으나, 항상 그런 것은 아니다.
그래도... 일반적으로 이들의 trade-off를 적당히 조절하는 게 중요하긴 하겠지..? 머신러닝에서..!

분산과 편향의 trade-off 관계를 어떻게 해결할 수 있을까?
해결 방법은 일반적으로 모델의 복잡도를 키우고, 과적합을 막는 방식으로 이루어진다.
지난 시간에 모델의 복잡도가 커지면 분산이 커지고 과적합이 될 수 있다고 배웠는데, 여기에서 과적합을 막기 위한 방법을 적용시키면 모델의 복잡도가 적당히 크고, 과적합은 잡아주는 그런 이상적인 모델이 되는 것...!
방법은 크게 3가지가 있다.
1) 검증 데이터셋(validation data)을 이용하는 것
2) k-폴드 교차검증
3) 정규화 손실 함수

검증 데이터셋 개념은 그리 어렵지 않다. 원래는 학습 데이터 80%, 평가 데이터 20%로 나눴다면, 이번엔 그 사이에 검증 데이터를 끼워 넣어서, 학습 80%, 검증 10%, 평가 10% 이런 식으로 구성하는 것을 말한다.
검증 데이터와 평가 데이터 모두 학습에 사용하지 않는다는 공통점이 있다.
둘의 차이는, 검증 데이터는 학습 결과를 중간 평가해서 최적의 파라미터를 찾는 데 사용하는 것이고 평가 데이터는 완전히 학습을 종료한 후 머신의 성능을 평가하는 것이라는 점이다.
약간.... 열심히 공부한 다음(train), 모의고사 치고(valid) 오답노트 한 다음에, 실제 수능(test)을 보는 느낌이랄까...?
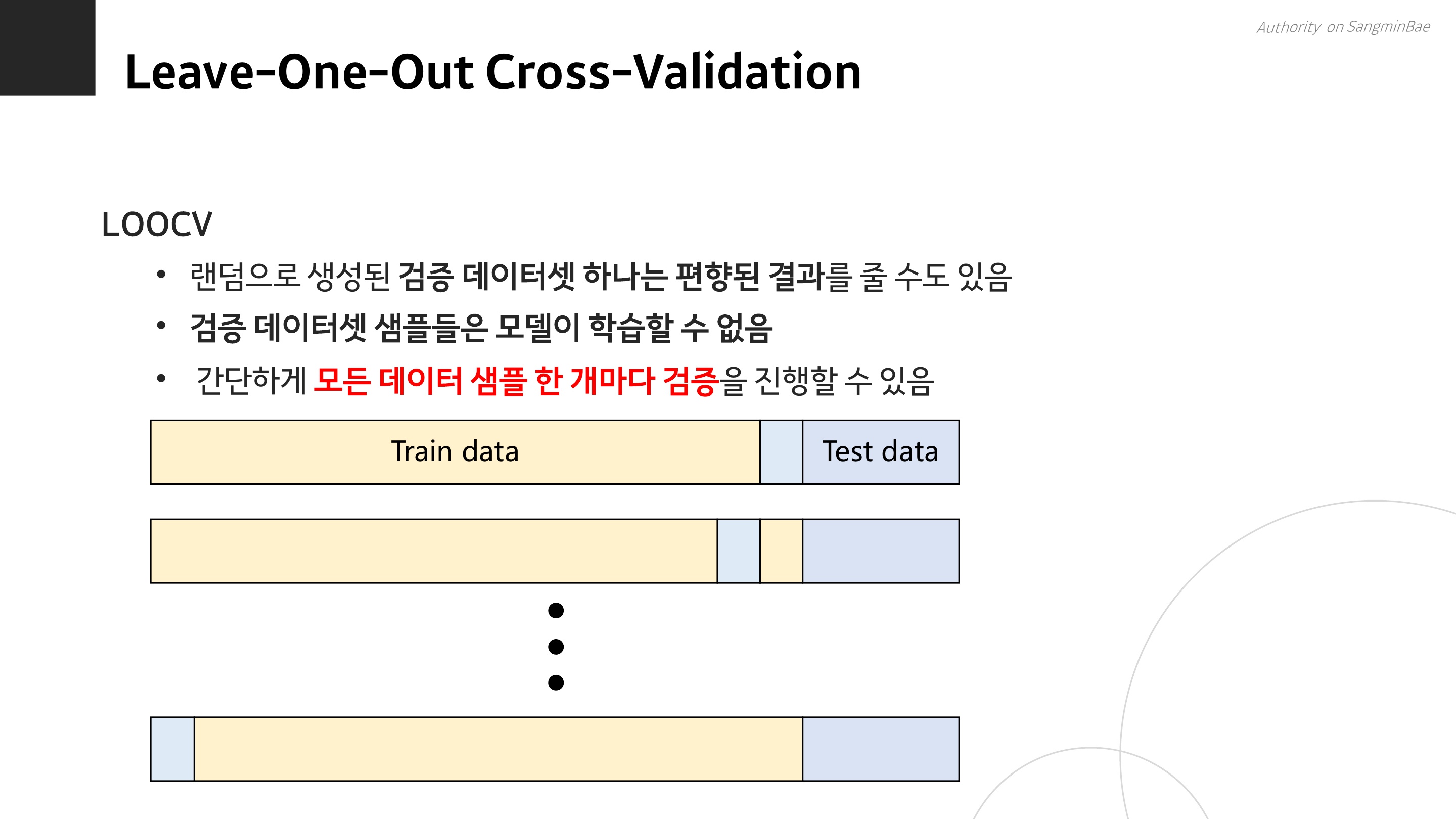
다음으로는, LOOCV 방식이 있다. 검증 데이터셋을 랜덤으로 10% 뽑아도, 검증을 딱 한 번만 하기 때문에 그 결과 자체에 편향이 있을 수 있다. 당연히...! 그리고 검증에 사용한 데이터는 학습에 쓸 수 없다는 아까운 상황이 발생한다.
그래서, 검증 데이터를 딱 하나만 남기고 나머지는 다 학습에 사용한 다음, 이를 데이터 수인 n번 반복하는 것을 LOOCV 방식이라고 한다.
단순히 N번이라 하면, 그렇구나... 하겠지만 3만 개의 행을 가진 데이터 셋이 있다면 30,000번 학습을 시켜야 하므로 계산비용이 어마어마하게 클 것이다. 이런 단점으로 인해 K-fold 방식이 나오게 되었다.
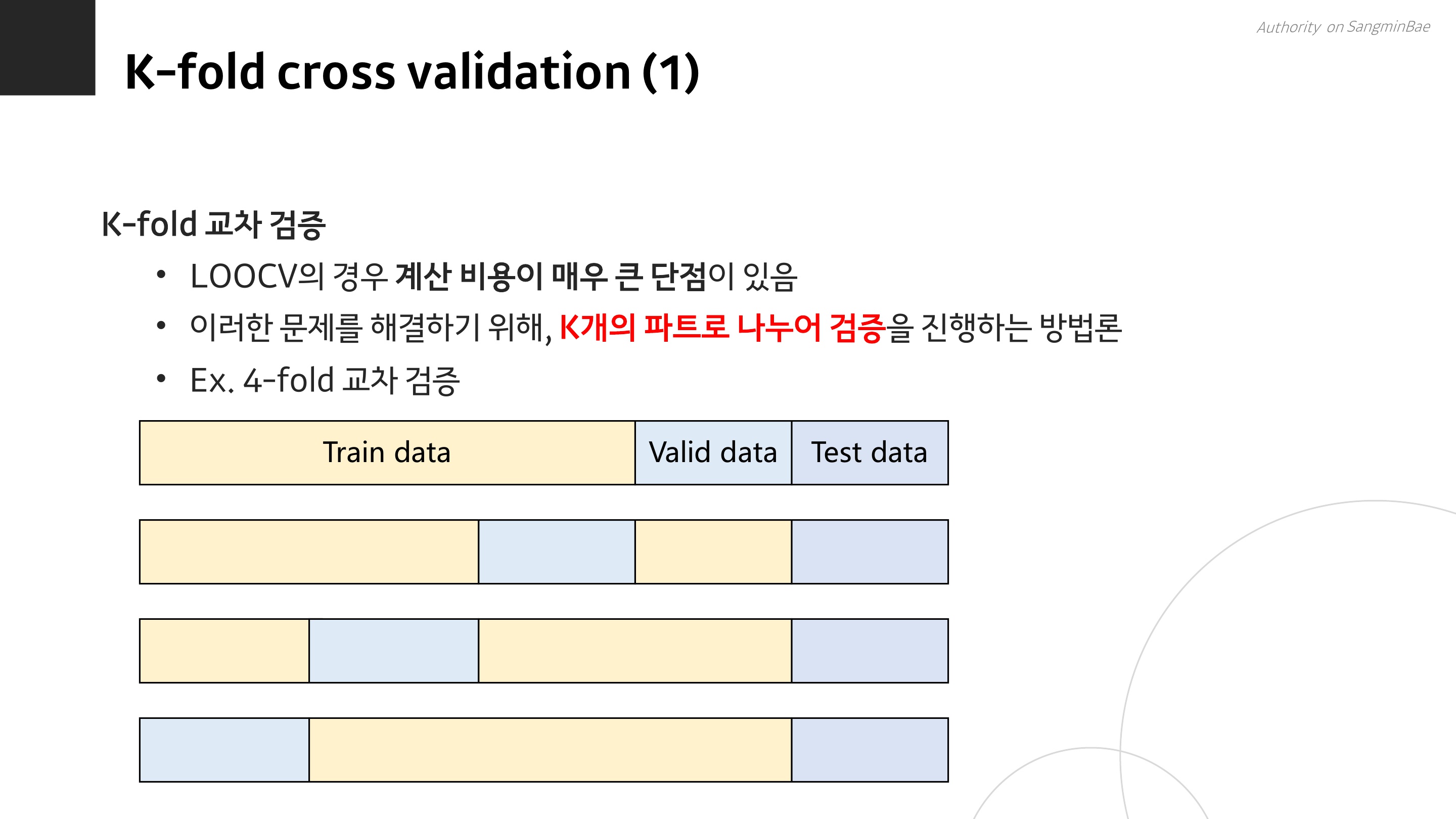
K-fold 교차 검증은 LOOCV의 어마어마한 계산비용 문제를 해결하기 위해 제안된 방법이다.
현실에서도 문제 하나를 해결하려 하면 또 다른 예상치 못한 문제가 발생하는 경우가 있지....! 절충안을 잘 찾아야지.
K-fold는 데이터셋 개수인 N만큼 반복 학습을 시키는 건 너무너무 많으니까, 그냥 좀 크게 K개의 덩어리로만 나누자~ 라고 합의를 본 것이다.
위 그림에서 나오는 예시는 k가 4인 4-fold 교차검증이다. 학습 데이터를 4등분해서, 그 중에 하나를 검증 데이터로 삼고, 또 다른 1/4을 검증 데이터로 하고, 또 다른 1/4, 또 다른 1/4을 검증해서 총 4번 학습과 검증을 거치는 것이다.
5개 모델에 대해 평가하고 싶을 때는 k를 5로 설정하면 된다. N번에 비하면 훨씬 훨씬 현실적이고 합리적인 방법인 것 같다...

여기에서 K값이 커지면 어떤 일이 벌어질까?
K값이 커진다는 것은, 얼마나 작은 등분으로 데이터를 나눌지를 의미한다. k=2이면 검증 데이터는 1/2이지만, k=100이면 검증 데이터는 1/100로 작아진다.
1) 즉, K가 커질수록 검증데이터셋 크기가 작아지고 학습에 사용할 수 있는 데이터 수는 많아진다.
2-1) 학습에 사용되는 데이터가 많은 만큼, 데이터의 전체 패턴을 모델이 이해하기 쉬워지므로 편향 에러는 줄어든다.
2-2) 반면, 모델의 예측 성능이 분할에 따라 엄청 민감하게 바뀔 것이므로 분산 에러는 커진다.
3) K값이 최대한으로 커지면 N과 같아질 것이다. 즉, LOOCV의 단점과 같이, 계산비용이 커진다.
원래라면 세 번째 방법인 Regularization(정규화)도 이 글에 같이 정리하면 좋은데, 넘 피곤해서 오늘은 생략... 언젠가 추가 하거나 다음 글에 쓰도록 하겠다. 다음주면 서포터즈 마지막 주다. 31일에 워크숍 가서 월, 화, 수 3일간 모든 일을 끝내야 한다. 휴휴.... 그래도 난생 처음 워크숍을 가는 거라 좀 기대가 된다. 마지막까지 서포터즈 마감기한을 바탕으로 동기부여하여... 파이팅...!🔥🔥
* 메타코드 서포터즈로서 강의를 제공받아 작성하였습니다. 이미지를 클릭하면 홈페이지로 이동합니다.
'빅데이터분석' 카테고리의 다른 글
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (8) MLE/MAP (5) | 2024.10.31 |
|---|---|
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (7) 로지스틱 회귀 (1) | 2024.10.31 |
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (5) 편향과 분산(Bias and Variance) (1) | 2024.10.27 |
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (4) 경사하강법(Gradient Descent) (1) | 2024.10.20 |
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (3) 선형 회귀(Linear Regression)와 최적화(optimization) (1) | 2024.10.20 |