🔥 메타코드에서 머신러닝 입문 부트캠프 강의를 듣고 있다. 머신러닝에 대한 전반적인 지식을 익히고, 내 손으로 하이퍼파라미터도 조정해보고 최적화된 모델을 찾기 위해!! 맨날 RandomForest만 돌리는 빅분기 취득자를 졸업하자!ㅁ! 아자아자!! 근데...? 머신러닝에서 사용되는 수학적 개념들을 배우다가 포기할 뻔 했다. ㅠㅠ 자연 상수, 시그모이드 함수, log와 미분 이야기들이 막 나오는데... 그래도 힘내봐야지. 서포터즈로 이왕 제공받은 강의 열심히 끝까지 들어보려고 한다. 강의를 듣고 나면 어려운 수학적 내용도 조금은 익숙해지지 않을까?
2. 회귀(Regression) - 머신러닝을 위한 기본 수학(Basic Math for ML)

함수란, 두 집합 사이의 관계 혹은 규칙을 말한다. y = f(x) 꼴로 표현된다.
일차함수는 모두들 아는 것처럼 y = ax + b 이고, 그래프로 그리면 직선 형태를 띈다. 기울기가 양수이면 올라가는 직선, 기울기가 음수이면 내려가는 직선...! 절편(b)은 y축과 만나는 점을 의미한다.
(여기까지는 끄덕끄덕 하면서 들었다. ㅋㅋ)

2차 함수도 아직 쉽다. 포물선 형태로 생겼고, y = a(x-p)^2 + q 형태로 표현된다. a가 양수면 아래로 볼록한 그래프, a가 음수이면 위로 볼록한 그래프가 그려진다. 함수의 꼭짓점은 (p, q)로 표현한다.
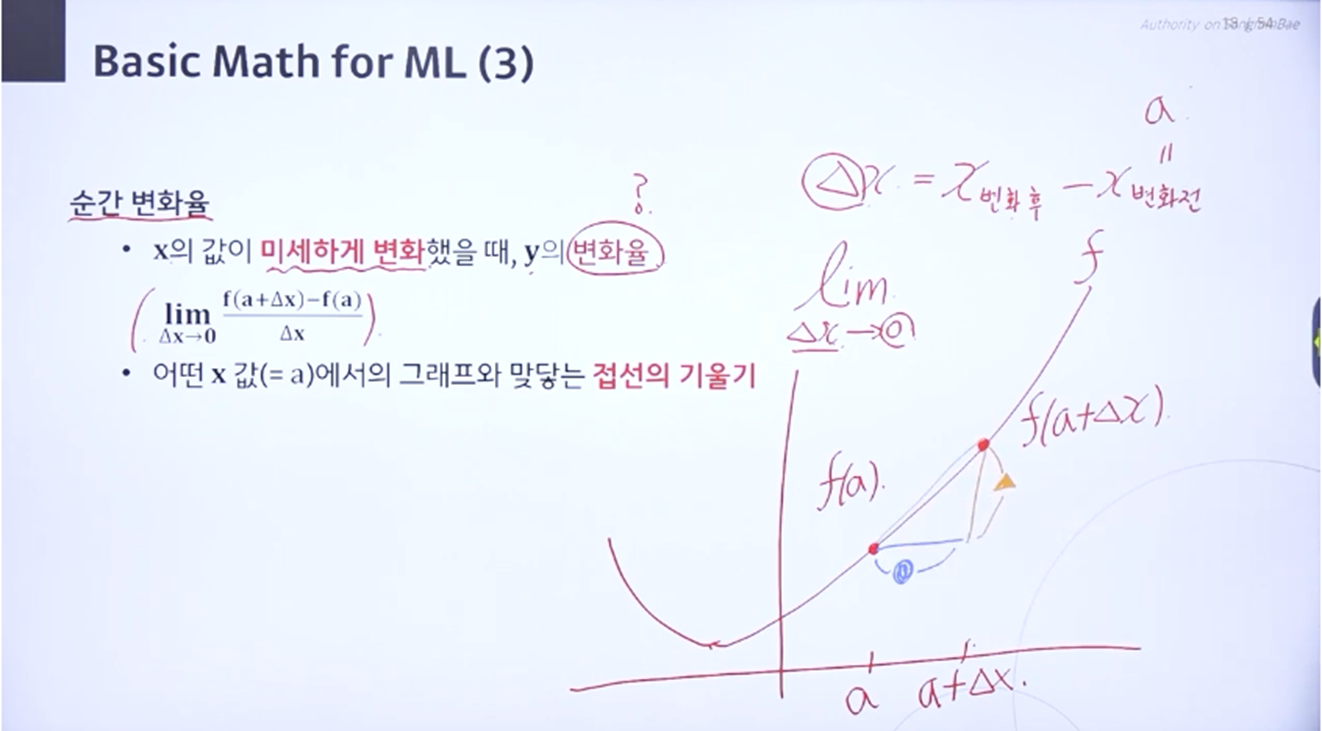
이제 순간 변화율이라는 개념이 나오는데, 정의상으로는 x가 미-세하게 변했을 때 y의 변화율을 의미한다.
위 이미지에서 그려주신 그래프를 보자. x = a인 지점에서 y 값은 f(a)가 된다. 여기에서 델타x 만큼 이동했을 때는 y = f(a+델타x) 가 되는데, 이 f(a)와 f(a+델타x)의 차이를 선으로 그어 보면 y가 얼마나 변했는지 알 수 있다.
이를 식으로 표현했을 때 순간변화율은 lim 델타x가 0으로 갈 때(x의 변화량이 아주아주아주 작아서 0으로 수렴할 때) 델타x(x의 변화량) 분에 f(a+델타x) - f(a)가 된다.
변화량이 무수히 작아졌기 때문에, 결국 어떤 값(x = a)에서 그래프와 맞닿는 접선의 기울기를 순간 변화율이라고 한다.

미분 이야기가 나오는데, 미분의 개념이 엄청 중요하다기 보다는 미분의 개념에서부터 함수의 최솟값이 가지는 특징이 나오기 때문에 미분을 알아야 한다.
미분은, 앞서 봤던 함수의 순간변화율을 구하는 것과 동일하다. f'(x) 또는 미분의 derivative를 써서 dx분의 d f(x)로 표기한다. 함수의 최솟값에서 미분값(순간변화율)은 항상 0이 된다. 2차 함수를 생각해 보면, 아래로 볼록한(약간 빗살무늬 토기모양...) 그래프의 가장 아래 꼭짓점에 접선을 그려보면 x축과 수평인 선이 그어질 것이다. 즉, 기울기가 0이 된다. :)
실제 y와 예측값 y(y^)의 차이를 손실값으로 정의한다면, 손실값을 최소화하는 파라미터를 찾는 것이 머신러닝의 목적이다. 손실함수의 순간변화율이 0이 되는 지점이 손실함수의 최솟값이 되므로, 이를 이용해서, 파라미터의 최적값을 구할 수 있다고 한다. 🙄 넘 어렵당

지수함수는 말 그대로 밑과 지수로 이루어진 함수인데, 지수 부분에 x가 들어간다.

자연상수...! 자연상수 개념을 나는 머신러닝 강의에서 처음 들었다.
자연상수 e는 n이 무한대로 늘어날 때 1+ 1/n의 n승을 말한다. 식이 왜 이따구야ㅠㅠ
log에서 밑이 표시되지 않으면 자연로그라고 부르는데, 이때 자연!이 자연상수 e를 뜻한다. 자연로그는 밑이 e이다.
자연상수는 파이처럼 수학에서 중요하게 쓰이는 무리수인데, 대략 2.718... 의 값을 갖는다.
어찌하여 2.718어쩌구가 되었는고 하면,
자연상수 e는 100% 성장률을 가지고 1회 연속 성장할 대 가질 수 있는 최대 성장량을 의미하는데,
예를 들어서 1원을 가지고 있는 사람에게 1년이 지나면 똑같이 1원을 줄게(100% 성장)라고 말했다고 치자.
그러면 1원을 가진 사람이 1년 뒤에 가지고 있는 돈은 2원이 된다.
만약 반년마다 돈을 받는다면 어떻게 될까? 1원을 가진 사람은 반년 뒤에 0.5원을 받아서 1.5원을 가지게 된다. 이 돈이 반년 뒤에 또 반씩 늘어나면, 1원의 반인 0.5원과 0.5원의 반인 0.25원이 늘어나서 총 0.75원 증가한, 2.25원을 가지게 된다.
오잉! 돈이 늘어났군?!... 마치 적금에서 단리/복리의 차이를 보는 것 같다. ㅇvㅇ 자연상수가 이런 개념이라니!.. 생각보다 어렵진 않은 것 같다.
반년만 나눠도 2원 -> 2.25원으로 늘어나는데 이걸 무한히 쪼개서 돈을 받는다고 치면 결국 2.718281828.... 이라는 값이 나온다고 한다.
자연상수 e의 중요한 특징은, 미분하면 자기 자신이 나온다는 것이다. :)

다음은 시그모이드 함수와 소프트맥스 함수다. 앞서, 시그모이드 함수는 이진분류에서, 소프트맥스 함수는 다중분류에서 사용된다고 했다. 먼저 시그모이드 함수를 보자. y = 1 - e의 -x승 분에 1로 표현된다.
x가 0일 때를 대입해보면, 어떤 수의 0승은 1이 되므로, e의 -x승은 1이 된다. 1/1+e^-x 식에 넣어 보면 1/2, 즉 0.5가 된다.
x가 무한대로 가면, e의 -무한대 승은 무수히 무수히 작은 수이기 때문에 e^-무한대는 0으로 수렴한다. 시그모이드 식에 넣으면 1/1+0 = 1
반대로 -무한대로 발산하면 e의 -(-무한대)승은 무한히 큰 수가 되고, 시그모이드 식에 넣었을 때 1/1+무한대 이므로, 무한대 분에 1은 0으로 수렴한다.
즉, 시그모이드 함수는 중앙값이 0.5이면서 0~1 사이인 독특한 함수가 된다.
챗 GPT가 나보다 설명을 잘한다.. 크흡...

소프트맥스 함수는 다중분류에서 사용되고, 0~k까지 클래스의 예측값을 받는다(예를 들어 A, B, O, AB형 처럼 3개 이상의 범주가 k개 있다는 뜻). 여기에서 각 범주가 나올 확률을 계산한다.
확률은 0과 1사이의 값을 가지면서, 가능한 모든 확률값을 더하면 1이 나와야 한다는 특징이 있다. 이를 활용한 게 소프트맥스 함수라는데 사실 이해를 엄청 제대로 한 것 같진 않다. 휴

로그함수는 지수함수 x = a^y의 역을 취하면 y = log a^x 가 된다고 한다. 신ㄱ...ㅣ
y = log a^x에서 밑이 적혀있지 않을 때는 자연로그(ln)로, 자연상수(e)를 밑으로 가진다고 생각하면 된다고 함.
이번에 정리한 수학적 개념은 좀 복잡했지만, 여러번 읽으면 그렇게 어렵지도 않은 것 같다.
다음엔 본격적으로 회귀 개념을 정리할 것 같다. 얼른 코드를 치고 싶다. ...
그럼 이만, 화르륵 🙄🔥🔥
* 메타코드 서포터즈로서 강의를 제공받아 작성하였습니다. 이미지를 클릭하면 홈페이지로 이동합니다.
'빅데이터분석' 카테고리의 다른 글
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (4) 경사하강법(Gradient Descent) (1) | 2024.10.20 |
|---|---|
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (3) 선형 회귀(Linear Regression)와 최적화(optimization) (1) | 2024.10.20 |
| [머신러닝] 메타코드 강의 후기_머신러닝 입문 부트캠프 (1) 인트로, 용어정리 (0) | 2024.10.13 |
| [powerBI] 메타코드 강의후기_(4) 가설설정 및 통계적 검정 (2) | 2024.10.06 |
| [powerBI] 메타코드 강의후기_(3) 기초통계 개념 (2) | 2024.10.06 |